 |
||||
|
Biblioteca Virtual
A) MAPAS COMO FORMAS DE REGISTRAR INFORMAÇÃO Imagine que você precise saber como ir de Vitória até o Rio de Janeiro. Você poderia consultar um mapa para obter tal informação. O mapa da figura 1 é usado com esse objetivo. Como qualquer tipo de mapa ele tem muitas limitações. Observe, por exemplo, que ele não traz nenhuma informação sobre o relevo ou sobre os rios brasileiros.
Como você sabe, há uma enorme variedade de tipos de mapas. Eles trazem diferentes tipos de informação, tais como clima, relevo, distâncias, posições geográficas e até detalhes sobre rodovias e ferrovias. Além dos mapas, diferentes formas de representação, originados nas ciências, foram integrados à linguagem de diversas áreas do conhecimento. São vários tipos de gráficos, tabelas, equações, esquemas e diagramas. Todos esses diferentes recursos têm a finalidade de registrar e exibir informações. São recursos de comunicação muito usados nos dias atuais, sendo encontrados, inclusive, em revistas e jornais.
B) SISTEMAS DE COORDENADAS RETANGULARES Vamos imaginar que um ônibus da linha Rio de Janeiro-Brasília / Brasília-Rio de Janeiro tenha “quebrado” após viajar 31 Km. O motorista avisa a central pelo telefone celular e pede para mandar um mecânico. A empresa mantém mecânicos tanto no Rio de Janeiro quanto em Brasília, e manda um carro de socorro da cidade mais próxima ao ponto no qual o ônibus “quebrou”. Para localizar o ônibus, sabendo que ele está na estrada que liga as duas cidades, é necessário fornecer apenas a distância a que ele se encontra de algum lugar. Essa situação é chamada de unidimensional, porque faz-se a localização do objeto “sobre uma linha”. Para localizar objetos “ao longo de uma linha”, como a estrada, é preciso escolher um ponto de referência a partir do qual serão medidas as distâncias. Nesse caso, é preciso escolher uma origem. A distância é medida a partir da origem. No caso de estradas estaduais, a origem é localizada em um dos extremos da estrada. Entretanto, a escolha do ponto de origem é apenas uma questão de conveniência ou convenção. O que você aprendeu sobre a localização de um veículo em uma estrada vale para a localização de qualquer objeto, ou mesmo para coisas abstratas como a divisa entre dois estados cortados por uma mesma estrada. A distância que você usa, nesse tipo de localização, acompanhada de uma unidade de medida correspondente, é chamada de coordenada de localização do objeto.
O exemplo da localização de um objeto em uma sala de aula pode nos ajudar a compreender como se procede em situações mais gerais. Digamos que você tenha que determinar a posição do ponto “A” marcado na figura 3. Tal ponto está localizado num espaço bidimensional que é a folha de papel. Para localizar cada ponto no espaço da folha, precisamos de duas coordenadas, ou seja, duas distâncias.
Em Física e em matemática usam-se um eixo horizontal, chamado eixo X, e um eixo vertical, chamado eixo Y, como referências para as coordenadas de localização dos pontos. O encontro dos dois eixos é a origem do sistema de coordenadas. A escolha do lugar onde situamos os eixos X e Y não importa muito. A distância entre os pontos A e B da figura 3, por exemplo, não é alterada quando se altera a posição dos eixos coordenados X e Y. Na utilização do sistema de coordenadas, há algumas convenções que são normalmente obedecidas:
Para facilitar a tarefa de localizar pontos num plano, pode-se usar uma folha de papel quadriculado ou milimetrado. Para evitar confusão sobre que número representa cada uma das coordenadas, convenciona-se que a coordenada x é sempre apresentada em primeiro lugar, seguida da coordenada y. No caso do ponto A da figura 4, a forma resumida de localização do ponto nos leva a A (x,y) = A (3,-2). Essa forma resumida de apresentação das coordenadas nos diz que o ponto A tem está 3 cm à direita da origem sobre o eixo X e 2 abaixo da origem sobre o eixo Y.
c) LATITUDE E LONGITUDE A localização de pontos e regiões sobre a superfície da Terra se faz a partir de duas coordenadas chamadas de latitude e longitude. O ponto preto assinalado na figura 5 mostra a latitude e a longitude da cidade de São Paulo. Os valores dessas coordenadas são, respectivamente, iguais a 23,5º (latitude) e 46,7º (longitude). Mas por que razão essas coordenadas são dadas em graus?
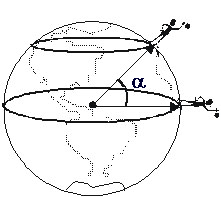
Podemos compreender a razão desse fato analisando a figura 6. Nela, vemos que a latitude de um ponto situado sobre a superfície da Terra corresponde ao ângulo a formado entre a linha que une o ponto ao centro da Terra e a linha que une o centro da Terra ao equador. O equador é sempre tomado como referência nas medidas de latitude. Análise semelhante a esta pode ser realizada para justificar o fato de que as medidas de longitude também são realizadas em graus.
A referência para a medida de longitude é o meridiano de Greenwhich em Londres, Inglaterra. A escolha dessa referência não é tão “natural” como a escolha do equador. Afinal, a linha do equador é uma referência definida pelo próprio movimento de rotação da Terra. No caso das linhas de longitude, a escolha da referência é mera convenção, não havendo razão física para que uma escolha qualquer seja considerada mais conveniente que a outra. Antes de Londres, a referência para a medida da longitude já esteve em Cabo Verde, Roma, Copenhague, Jerusalém, São Petersburgo, Pisa, Paris e Filadélfia, entre outros locais.
|
As
limitações dos mapas têm uma importante consequência: há vários
tipos de mapa que fornecem diferentes tipos de informação. O grau
de detalhamento das informações contidas em cada mapa varia em função
dos objetivos a partir dos quais ele foi elaborado. 
Se
puder, FAÇA AGORA MESMO a atividade “Localize
o ponto ou pague o mico” sugerida na página 26 deste
fascículo.
